x <- rnorm(1000)
qqnorm(x)
qqline(x)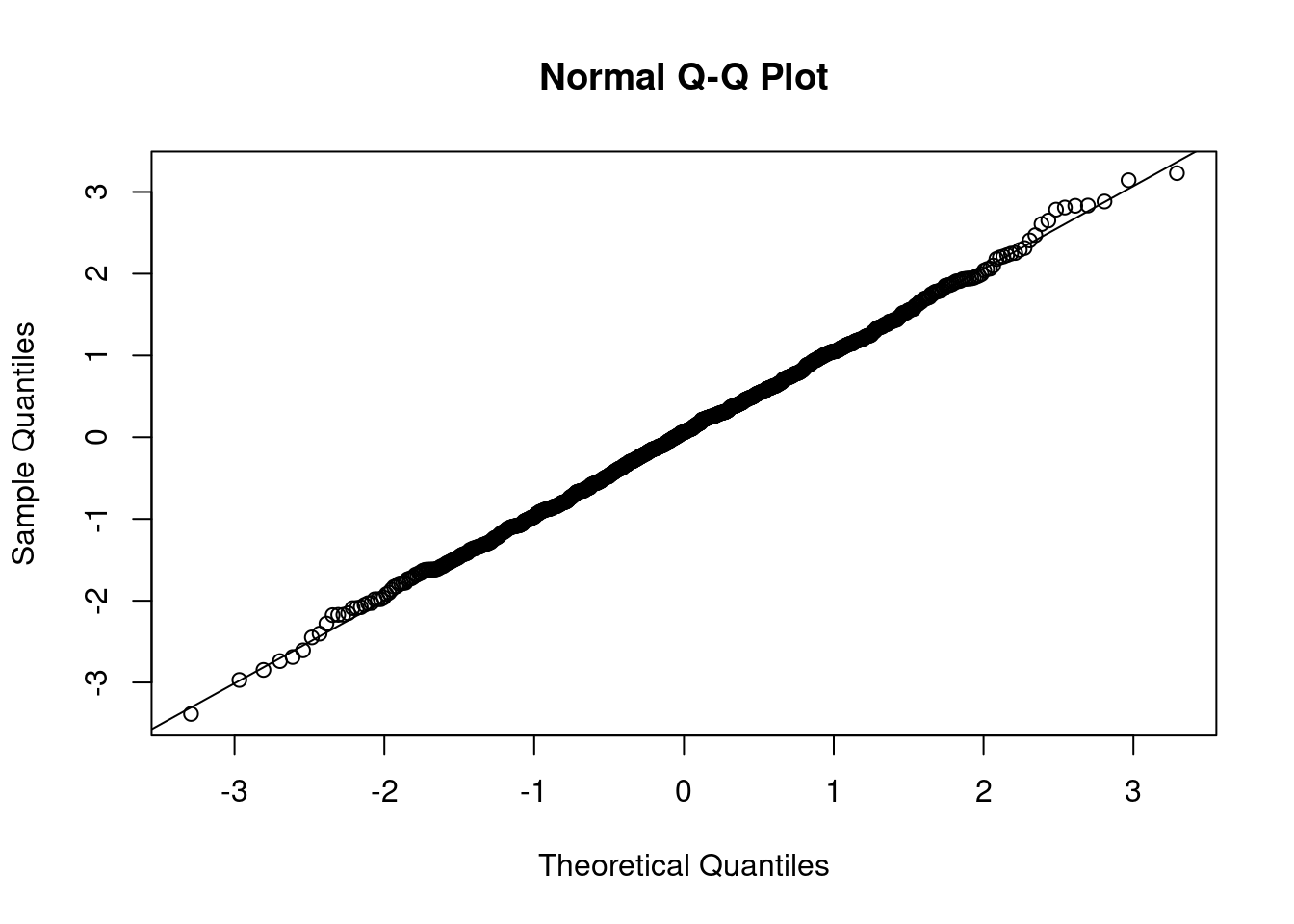
November 8, 2022
Open Intro Statistics Book:
HW 6 will be posted at the end of the week.
A claim about the value of a certain parameter, a set of parameters, or a distribution.
The null hypothesis is the claim that is initially believed to be true. For the most part, it is always equal to the hypothesized value.
The alternative hypothesis contradicts the null hypothesis.
| Null Hypothesis | Alternative Hypothesis |
|---|---|
| \(H_0: \mu=\mu_0\) | \(H_a: \mu\ne\mu_0\) |
| \(H_0: \mu\le\mu_0\) | \(H_a: \mu>\mu_0\) |
| \(H_0: \mu\ge\mu_0\) | \(H_0: \mu<\mu_0\) |
A hypothesis test is a statistical procedure to determine whether the null hypothesis is true or not. If we find that the null hypothesis is true, we claim: Fail to reject the null hypothesis. If we find the the null hypothesis to be false, we claim : Reject the null hypothesis.
To conduct a hypothesis test, we compute a test statistic based on the distribution of the null hypothesis. Then we determine if the test statistic is in the rejection region of the distribution of the null hypothesis. If it is in the rejection region, we reject the null hypothesis. Otherwise we fail to reject the null hypothesis.
The rejection region is determined by our \(\alpha\) value. \(\alpha\) determines the probability you are willing to be wrong if you reject the null hypothesis. This probability is something you want to set yourself at the beginning of a study. In general, the majority of researched set this to be \(\alpha=0.05\).
| Test | # of Samples | Null Hypothesis | Distribution | DF | Test Statistics | Notes |
|---|---|---|---|---|---|---|
| t-test | 1 | \(\mu=\mu_0\) | \(t_{DF}\) | \(DF=n-1\) | \(\frac{\bar X-\mu_0}{\sqrt{s^2/n}}\) | \(n<30\) |
| z-test | 1 | \(\mu=\mu_0\) | \(N(0,1)\) | None | \(\frac{\bar X-\mu_0}{\sqrt{\sigma^2/n}}\) | \(n>30\) \(\sigma^2\) known |
| z-test | 1 | \(\mu=\mu_0\) | \(N(0,1)\) | None | \(\frac{\bar X-\mu_0}{\sqrt{s^2/n}}\) | \(n>30\) \(\sigma^2\) unknown |
| paired t-test | 2 | \(\mu_1-\mu_2=D\) | \(t_{DF}\) | \(DF=n-1\) | \(\frac{\bar X_d-D}{\sqrt{s_d^2/n}}\) | \(n\) is the number of pairs |
| independent t-test | 2 | \(\mu_1-\mu_2=D\) | \(t_{DF}\) | \(DF=n_1+n_2-2\) | \(\frac{\bar X_1-\bar X_2-D}{\sqrt{s_p^2(1/n_1+1/n_2)}}\) | \(s_p^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}\) |
| independent t-test | 2 | \(\mu_1-\mu_2=D\) | \(t_{DF}\) | \(DF=\frac{(s^2_1/n_1+s^2_2/n_2)^2}{(s^2_1/n_1)^2/(n_1-1)+(s^2_2/n_2)^2/(n_2-1)}\) | \(\frac{\bar X_1-\bar X_2-D}{\sqrt{s_1^2/n_1+s^2_2/n_2}}\) |
Notice how there are 3 types of null and alternative hypothesis, The first type of hypothesis (\(H_a:\mu\ne\mu_0\)) is considered a 2-sided hypothesis because the rejection region is located in 2 regions. The remaining two hypotheses are considered 1-sided because the rejection region is located on one side of the distribution.
| Null Hypothesis | Alternative Hypothesis | Side |
|---|---|---|
| \(H_0: \mu=\mu_0\) | \(H_a: \mu\ne\mu_0\) | 2-sided |
| \(H_0: \mu\le\mu_0\) | \(H_a: \mu>\mu_0\) | 1-sided |
| \(H_0: \mu\ge\mu_0\) | \(H_0: \mu<\mu_0\) | 1-sided |
Depending on the type of test and alternative hypothesis, you may be asked to conduct the test using a critical value. This approach will require you to compute the test statistic (denoted as \(T(x)\)) and and compare it with a critical value(s). Depending on you alternative hypothesis and \(\alpha\), you will reject the null hypothesis based on the following table:
| Alternative Hypothesis | Rejection Region | Critical value |
|---|---|---|
| \(\mu>\mu_0\) | \(T(x)>CV\) | \(P(X>CV)=\alpha\) |
| \(\mu<\mu_0\) | \(T(x)<CV\) | \(P(X<CV)=\alpha\) |
| \(\mu\ne\mu_0\) | \(T(X)<CV_1\) or \(T(X)>CV_2\) | \(P(X<CV_1)=\alpha/2\) and \(P(X>CV_2)=\alpha/2\) |
The p-value approach is one of the most common methods to report significant results. It is easier to interpret the p-value because it provides the probability of observing our test statistics, or something more extreme, given that the null hypothesis is true. Depending on the type of test, your p-value may be constructed as:
| Alternative Hypothesis | p-value |
|---|---|
| \(\mu>\mu_0\) | \(P(X>T(x))=p\) |
| \(\mu<\mu_0\) | \(P(X<T(x))=p\) |
| \(\mu\ne\mu_0\) | \(2\times P(X>|T(X)|)=p\) |
If \(p < \alpha\), then you reject \(H_0\); otherwise, you will fail to reject \(H_0\).
The confidence interval approach can evaluate a hypothesis test where the alternative hypothesis is \(\mu\ne\mu_0\). For this approach you will construct a \((1-\alpha)100\%\) confidence interval as
\[ PE \pm CV *SE \]
where PE is the point estimate, CV is the critical value based on \(\alpha\) and SE is the standard error. This will result in a lower and upper bound denoted as: \((LB, UB)\). The confidence intervals provides a range values to capture the parameter \(\mu\) such that if you repeat this process \(n\) times, \((1-\alpha)100\%\) of \(n\) will capture the true value of \(\mu\). If \(\mu_0 \in (LB,UB)\), then you fail to reject \(H_0\). If \(\mu_0\notin (LB,UB)\), then you reject \(H_0\).
QQ plot
Shapiro-Wilks Test
QQ plot
Shapiro-Wilks Test
QQ plot
Shapiro-Wilks Test
F-test
Bartlett’s Test
Levene’s Test
A qq (quantile-quantile) plot will plot the sample quantiles from the data versus the theoretical quantiles from an normal distribution. If the data comes from a normal distribution, then the points should line up to \(y=x\) line. The following code runs a qq plot from data generated from a standard normal distribution:
The Shapiro-Wilks Test is a hypothesis test to determine if the data comes from a normal distribution. It tests the following hypothesis
| \(H_0\) | \(H_1\) |
|---|---|
| The data comes from a normal distribution. | The data does not come from a normal distribution. |
This test will result in a p-value that can be used to conduct the hypothesis test. The following code runs a Shapiro-Wilks test on data generated from a standard normal distribution:
An F-test is hypothesis test to see if the variances are equal or not. It has the following Hypothesis:
| \(H_0\) | \(H_1\) |
|---|---|
| \(\frac{\sigma^2_1}{\sigma^2_2}=1\) | \(\frac{\sigma^2_1}{\sigma^2_2}\ne1\) |
This test will result in a p-value that can be used to conduct the hypothesis test. The following code runs an F-test on data generated from a standard normal distribution:
F test to compare two variances
data: x and y
F = 4.1342, num df = 999, denom df = 999, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
3.651745 4.680425
sample estimates:
ratio of variances
4.134213 Both Bartlett’s and Levene’s test the following hypothesis for equal variances:
| \(H_0\) | \(H_1\) |
|---|---|
| The variance are equal to each other. | The variances are not equal to each other. |
This test will result in a p-value that can be used to conduct the hypothesis test. The following code runs a Bartlett’s and Levene’s test on data generated from a standard normal distribution:
x <- rnorm(1000)
y <- rnorm(1000, sd = 0.5)
z <- c(x,y)
g <- rep(c(0,1),each=1000)
bartlett.test(z, g)
Bartlett test of homogeneity of variances
data: z and g
Bartlett's K-squared = 483, df = 1, p-value < 2.2e-16library(car) # Levene's test is found in the car package, you may need to install it
leveneTest(z, g)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 377.19 < 2.2e-16 ***
1998
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1| Playlist | Playlists | Notes |
|---|---|---|
| Hypothesis Testing | Videos | |
| Hypothesis Testing Examples | Videos | |
| Hypothesis Test Assumptions | Videos |
Wednesday R Code: File